Procedural Abstraction

上一个note提到了牛顿法求平方根。虽然能够工作，然而却有一些问题。看下面的代码 bad

(define (sqrt x)
  (define (improve guess)
    (/ (+ guess (/ x guess)) 2))
  (define (good-enough? guess)
    (if (< (abs (- (* guess guess) x)) 0.001) #t #f))
  (define (sqrt-iter guess)
    (if (good-enough? guess)
        guess
        (sqrt-iter (improve guess))))
  (sqrt-iter 1.0))

这部分代码的功能和之前note中提到的完全相同，不同点是前面提到的将sqrt这一问题划分为若干个自问题，的但是如果你认真的比较，你就会发现，这两快代码中最关键的部分都是goog-enough?中的(* guess guess)片段，这一片段决定了这段代码的结果。保持其他的结构不变，单独把(* guess guess)提取出来，以square过程表示，那么整段代码完全不关心square的实现，只需要知道它能计算平方即可。那么，与其说square是一个过程，不如说它是一种抽象，即*过程抽象*。

当然，最明显的区别是，这里的代码将前面的所有过程都集中到了一起，并且在内部定义的过程的参数也直接使用了在过程中传递的x。这样做的目的是避免对全局环境的影响，对用户而言sqrt就是sqrt，其他的过程会干扰他们大的思维。
acceptable

(define (sqrt2 x)
  (define (improve guess)
    (/ (+ guess (/ x guess)) 2))
  (define (good-enough? guess old)
    (if (< (/ (abs (- guess old)) old) 0.001) #t #f))
  (define (sqrt-iter guess old)
    (cond
      [(zero? x) x]
      [else (if (good-enough? guess old)
        guess
        (sqrt-iter (improve guess) guess))]))
  (sqrt-iter (improve 1.0) 1.0))

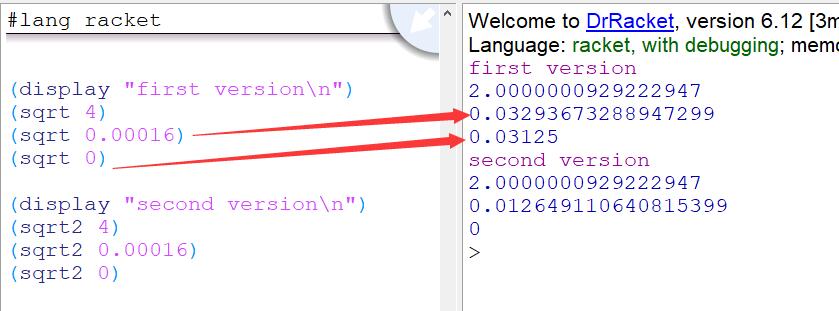
这段代码和上面代码通常情况下没什么区别，但在传入参数很小时，上面的代码会出现明显的错误

to be continued…