write an `apply` function from scratch

preface

Some of you may already used the std::apply from standard library, it accept a functor and a tuple then invoke functor with that tuple, I’ve been used it in some code such as:

a coroutine implementation

t1

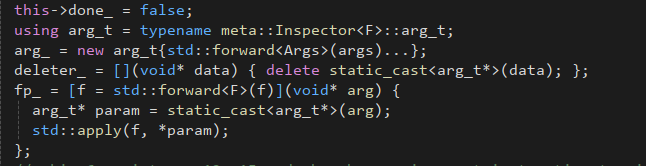
a functor-map implementation

t2

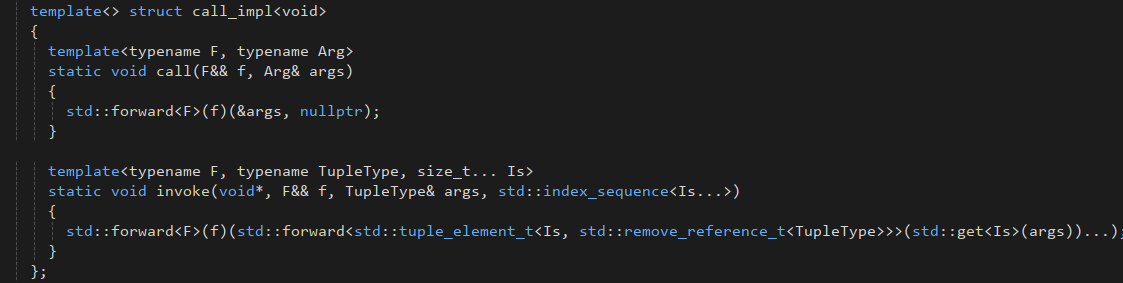
it’s very useful for library writer.

For almost two months not playing with c plus plus, I wonder if I can still write some meta-program, so I starting with the simplest index_sequence. unfortunately, I succeed not until several attempts, it’s really a shame. Then I start doing something more complicated, the apply function.

index sequence

An index sequence here is a template class with a sequence of non-type template parameters, the signature is:

template<size_t...> struct sequence

as we all know that meta-program is running at compile time, everything is constant, you can get an array value by

constexpr size_t idx = 0;
constexpr int x = arr[idx];

the constexpr keyword is required for idx , sequence can be treat as a collection of idx.

Template meta-programming is heavily rely on template recursion, just like normal recursion, the most important thing is when to stop the recursion. knowing that we can write the base case(where recursion stopped)

template<size_t> struct gen_seq; // declaration
template<> struct gen_seq<1> { using type = sequence<0>; }

here we can simply think sequence is the result and gen_seq is the function that produce sequence . we stop the recursion when size is 1 and the result is sequence<0> ,at this point we create a zero based index sequence. let’s start the recursion:

template<typename, typename> struct concat;
template<size_t... I1, size_t... I2> struct concat<sequence<I1..., I2...>>
{
  using type = sequence<I1..., (sizeof...(I1) + I2)...>;
};
// implementation
template<size_t N> gen_seq
{
  using type = concat<typename gen_seq<N/2>::type, typename gen_seq<N-N/2>::type>::type;
}

here we use a helper class concat to concatenate the left and right parts, by the way it has a log(n) time complexity.

and the last we create an alias

template<size_t N> using make_sequence = typename gen_seq<N>::type

tuple

Tuple is another popular class for meta-programming, it’s a heterogeneous container which means it can store elements with different types. it’s also useful for returning multiple values, especially when you can use the structured binding feature, then you can write something like:

auto foo() -> tuple<string, int, string>
{
  return {"elder", 1926, "+1s"};
}
int main()
{
  auto [name, age, motto] = foo();
  cout << name << ' ' << age << motto << '\n';
}

In meta-programming, tuple is used to hold the parameters which will be used later. to get tuple element one can write:

tuple t{"elder", 1926, "+1s"};
auto x = get<1>(t);

the index for get must be constant which knows at compile time(constexpr or literals), that’s why we need sequence.

We are facing a problem when implement tuple, that is: should we store the value directly? it’s not necessary for simple use case, but it’s not easy when you want specify the copy/move behavior. here we use an indirection:

template<typename T> tuple_val { T value; };

If you ever read Modern C++ Design by Andrei Alexandrescu, you will notice that implement a tuple is very easy(simply using multiple inherit):

template<typename...> struct tuple; // decleration
template<> struct tuple<> {}; // full specialization
template<typename T, typename... Ts> struct tuple<T, Ts...> : tuple<Ts...> // partial specialization
{
  using base = tuple<Ts...>;
  tuple_val<T> value;
  constexpr static size_t size = sizeof...(Ts) + 1;
  tuple(T&& t, Ts&&... ts) : base{forward<Ts>(ts)...}, value{forward<T>(t)} {}
};

for convenience we create a deduce guide:

template<typename T, typename... Ts> tuple(T&, Ts&&...) -> tuple<T, Ts...>;

notice that we use forward here, it’s necessary since one may pass data by value, lvalue or rvalue, and we must correct detect the real type then pass to next template, here is the code:

template<typename T> constexpr T&& forward(remove_ref_t<T>& x) { return static_cast<T&&>(x); }
template<typename T> constexpr T&& forward(remove_ref_t<T>&& x) { return static_cast<T&&>(x); }

by the way std::move is equivalent to the first forward .

element

To access value that store in tuple, we need a helper and it’s also a simple class

template<typename> constexpr bool false_t = false;
template<size_t Idx, typename T> struct element;
template<size_t Idx> struct element<Idx, tuple<>>
{
	static_assert(false_t<Idx>, "out of range");
};
template<typename T, typename... Ts> struct element<0, tuple<T, Ts...>>
{
  using type = T;
  using base = tuple<T, Ts...>;
};
template<size_t Idx, typename T, typename... Ts>
struct element<Idx, tuple<T, Ts...>> : element<Idx-1, tuple<Ts...>> {};
template<size_t Idx, typename... Ts> using element_t = typename element<Idx, Ts...>::type

It maintains two things, one is the type another is the base class . so giving an index and a tuple, we can get value type of current tuple and the base type of current tuple.

NOTE: the fasle_t is a common trick, you can’t simply write static_assert(false, "blablabla...") it will cause compilation error immediately, but once you take type into account, then the value is rely on template evaluation, the template is not evaluate then there’s no error.

get

We are almost prepared except retrieve data from tuple. here we write the getter

template<size_t Idx, typename... Ts> constexpr auto& get(tuple<Ts...>& x)
{
  using base = typename element<Idx, tuple<Ts...>>::base;
  return static_cast<base&>(x).value.value;
}

the return type is actually element_t<Idx, tuple<Ts...>>& , looking back to element implementation, we can find the fact:

The function body use static_cast cast x to it base class type and return base class member value, since the tuple is built-up by inheritance.

apply

Finally, the apply

template<typename R, typename F, typename Tuple>
R apply(F&& f, Tuple&& args)
{
  return [f = ::forward<F>(f), &args]<size_t... Is>(sequence<Is...>) {
    return f(::forward<element_t<Is, remove_ref_t<Tuple>>>(get<Is>(args))...);
  }(make_sequence<remove_ref_t<Tuple>::size>{});
}

no surprise, it looks like the second picture without passing index_sequence. let’s run it:

t3

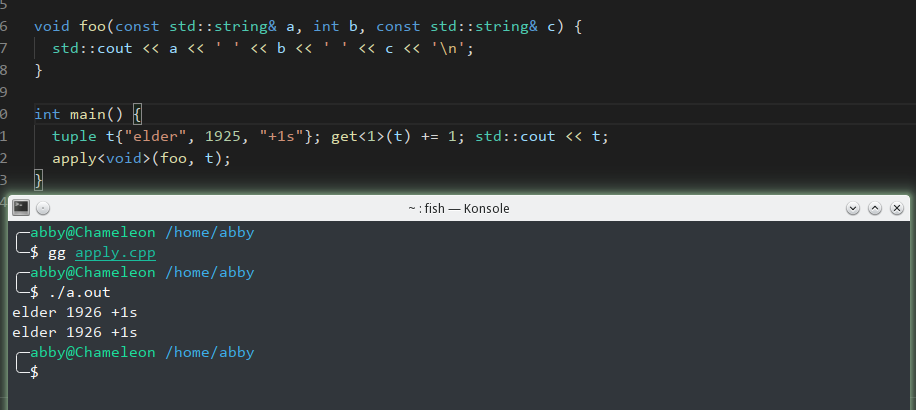
conclusion

it’s nothing, just some kind of practice.

code see apply.cpp